Над 1000 доктори на наука погрешно одговорија на овој логички проблем: Ако можете подобро од нив - Вие сте гениј

Уште во 70-тите години на минатиот век, плодниот статистичар Стив Селвин испратил писмо до американско списание за статистика со наслов „Проблемот во веројатноста“ во кое презентира интересна хипотетичка ситуација со предложено решение.
Откако доби бројни критики од своите колеги статистичари, тој испрати следно решение кое го нарече „Проблемот Монти Хол“ т.е. „Парадоксот на Монтихол“ според популарниот водител на квиз шоу од таа ера „Ајде да се договориме“, пишува порталот Медиум Дејли Дајгест.
Овој интересен случај можеби ќе беше заборавен доколку 15 години подоцна, во 1990 година, Мерилин Вос Савант, поранешна Гинисова рекордерка за највисок коефициент на интелигенција досега, не го споделила проблемот во нејзината популарна колумна „Прашај ја Мерилин“ во „Парада“ списание.
Резултатот?
Речиси 10.000 претежно лути писма влегоа во редакцијата на списанието, вклучително и над 1.000 од доктори на науки, а огромното мнозинство тврдеше дека Мерилин очигледно не била во право.
Што може да инспирира толку многу луѓе, од кои многумина најобразованите во Америка, да се откажат од своето драгоцено време само за да известат списание дека не е во ред да се пишува за нешто толку тривијално?
Па, точно - парадоксот на Монтихол!
Што е парадоксот на Монтихол?
Замислете дека сте гостин во квиз, а пред вас има три врати. Зад нив се три потенцијални награди - две кози и светкав спортски автомобил. Домаќинот знае кои награди се зад која врата, но вие, се разбира, не знаете.
Потоа играта оди вака:
Дозволено е да изберете една врата што сакате да ја отворите и зад која мислите дека се крие автомобилот. Домаќинот потоа отвора една од двете преостанати затворени врати. Откако ќе се отвори вратата и ќе видите коза зад неа, домаќинот прашува дали сакате да го промените изборот на врата или да оставите сè како што е. По вашата одлука, домаќинот ја отвора вратата што сте ја одбрале и дознавате дали сте добиле коза или автомобил.
Прашањето е: Дали имате поголеми шанси да го освоите автомобилот ако го промените вашиот избор или ако се држите до вашиот оригинален одговор?
Иако на прв поглед не изгледа така, одговорот е - ДА, АПСОЛУТНО ТРЕБА ДА ГО СМЕНЕТЕ ИЗБОРОТ НА ВРАТА! Затоа што е поголема веројатноста да освоите автомобил ако ја смените вратата наместо да го задржите вашиот првичен избор.
Ако го задржите вашиот првичен избор на врати, шансата тркачки автомобил да биде зад е 1/3. Ако го промените вашиот избор, имате 2/3 шанси да го освоите автомобилот.
Што е „финтата“?
Сега, ако сте како повеќето луѓе, ќе претпоставите дека не е важно дали ќе го промените одговорот или не. Затоа што - ако ни преостанат две врати, со само една коза и една кола, шансите мора да бидат 50%. Два избора, два исхода, случајноста имплицира дека тоа е како превртување паричка, нели?
Па не! Може и математички да се докаже дека ако го промените вашиот избор од првата врата на преостанатата неотворена врата, вашите шанси за победа се зголемуваат! Еве објаснување:
Кога ќе ја започнете играта, имате три избори со еднакви шанси да го освоите автомобилот, секој со 1/3 шанси за правилно погодување.
- Врата бр. 1 (затворена): 1/3 шанса
- Врата бр. 2 (затворена): 1/3 шанса
- Врата бр. 3 (затворена): 1/3 шанса
Но, тогаш водителката ја менува околината, додава информации - отвора врата зад која нема автомобил. Тоа ви остава избор од две врати. Ова е моментот кога здравиот разум почнува да ве изневерува. Ние природно мислиме дека имаме 50% шанси да го освоиме автомобилот, без разлика дали ќе го промениме нашиот избор или не! Но, еве што вели математиката…
На стартот, шансите се навистина 1/3, 1/3, 1/3. Значи, кога ја избравме вратата број 1, шансите беа навистина 1/3. Но, кога се отвори врата со коза, а не со автомобил зад неа, шансите се променија едноставно затоа што гејмастерот свесно ја избрал таа врата. Неговиот избор не беше случаен!
Оригинален избор:
- Врата бр. 1 (затворена): 1/3 шанса
- Врата #2 (затворена): 1/3 шанса
- Врата бр. 3 (затворена): 1/3 шанса
Но:
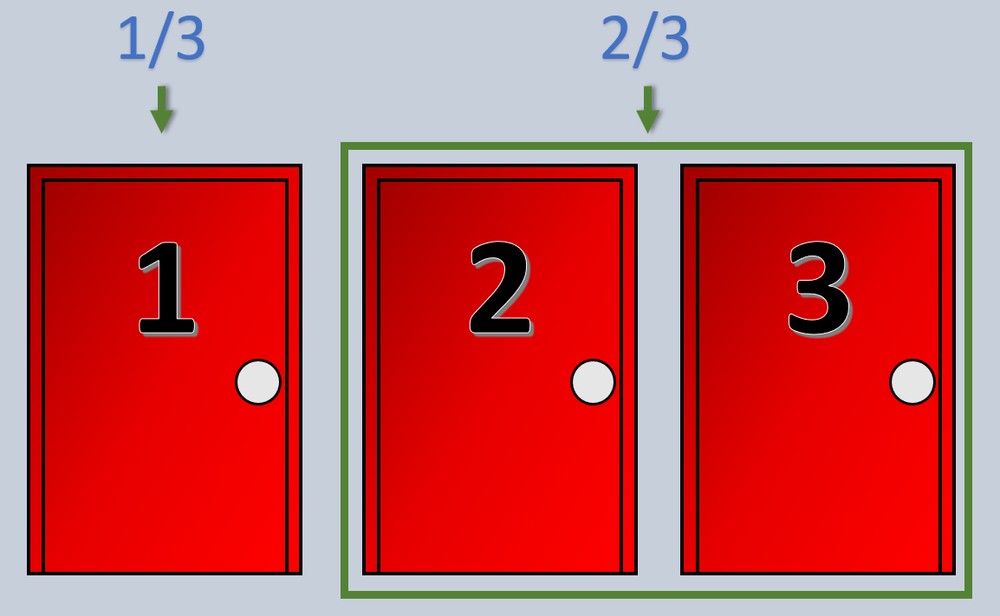
Ако мислиме на вратите #2 и #3 како комбинирани, сите можеме да се согласиме дека е 2/3, нели? Така, размислувајќи вака, кога водителот на емисијата ќе отвори врата за која знае дека зад неа има коза, завршуваме со:
- Врата бр. 1 (затворена): 1/3 шанса
- Врата #2 (затворена) + Врата #3 (отворена): 2/3 шанса да имате автомобил!

Ако го промените вашиот одговор од врата #1 на врата #2, вашите шанси се зголемуваат на 2/3! Погледнете го и графички:

Лудо, нели?
Доколку се уште не ви е јасно како настанува овој парадокс, погледнете го видеото: